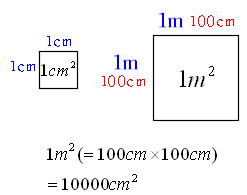
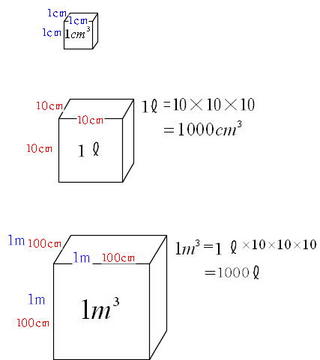
形の同じ三角形を見つけたら、比を使って解いていきます(形が同じ図形のことを相似(そうじ)といいます)。
辺の長さは違っても角度がそれぞれ等しいとき、2つの三角形は形が等しいといえます。
そして、形が等しいとき、2つの三角形の辺の比は等しくなります。
例題1:2つの三角形の形が等しいとき、xの値を求めなさい。
 図で、同じ色の角は角度が等しいことを表わしています。角度の等しい三角形は、形が等しいといえます。形が等しいとき、対応する辺の比も等しくなります。
図で、同じ色の角は角度が等しいことを表わしています。角度の等しい三角形は、形が等しいといえます。形が等しいとき、対応する辺の比も等しくなります。
(2つの角の大きさが等ければ、三角形の3つの角の和は180度なので、色のついていない角どうしも同じ大きさです。)
左の三角形の12cmが、右の三角形だと18cmにあたりますから、右の三角形の辺の長さは左の三角形の辺の18÷12=1.5倍です。
だから、xは8×1.5=12cm。
比例式を使って解くのもよい方法です。
12:18=8:x
比例式では、内側同士の積と外側同士の積は等しいので
12×x=18×8
x=18×8÷12
x=12
例題1の2つの三角形は、見ただけですぐに形が等しい(相似)とわかりますが、気づきにくいもののほうがよく出題されます。
形が等しい三角形を見つけるコツは、角の等しい三角形を発見することです。
例題2:次の図形で、どの三角形とどの三角形の形が等しいか(=相似か)、見つけてください。
1、
 平行に気づき、等しい角を見つける(その1)
平行に気づき、等しい角を見つける(その1)
左の図で、赤色の直線どうしは平行です。どの図形とどの図形が相似でしょうか?
 平行な2本の直線があるとき、等しい角を見つけておきます。
平行な2本の直線があるとき、等しい角を見つけておきます。
左下の角どうし、右下の角どうしが等しくなります(同位角といいます。頂上の角も共通な角なので等しくなります。)
角度が等しいので、小さい三角形と大きい三角形の形が等しくなります。
2、
 平行に気づき、等しい角を見つける(その2)
平行に気づき、等しい角を見つける(その2)
左の図の四角形は長方形(正方形でも考え方は同じ)です。
左の図の中には、お互いの形が等しい三角形の組が3組あります。見つけてください。
 1番の問題と同じ要領で、平行な2本の直線を手がかりに、等しい角をもつ三角形どうしを見つけます。
1番の問題と同じ要領で、平行な2本の直線を手がかりに、等しい角をもつ三角形どうしを見つけます。
左の3組が、形の等しい三角形の組み合わせになります。
赤色と赤色、青色と青色の角どうしが等しい角です(さっ角といいます)。
1番と違い、ここで見つけた図形は、問題を解くときに、形が等しいこと、比を使えることに気づきにくいものばかりです。ある程度問題数をこなして、問題に慣れることが必要です。
3、
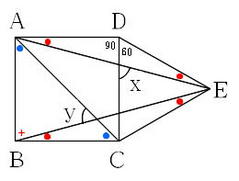
 直角三角形で、等しい角を見つける
直角三角形で、等しい角を見つける
左の図の中には、形の等しい三角形が何個あるでしょうか?
 直角で1つの角が等しくなり、あと1つ、角が共通であれば、すべての角が等しいことになります。
直角で1つの角が等しくなり、あと1つ、角が共通であれば、すべての角が等しいことになります。
つまり、直角三角形の中にある直角三角形は、すべて、もとの三角形と相似です。
では、確認問題をしてみましょう。
例題3:次の図形で、辺xの長さはいくらになりますか。
(1)

(解答)形の等しい三角形どうしの辺を考えないといけません。12cmは三角形の辺ではありません。大きな三角形の辺は6+12=18cmです。
小さい三角形の6cmが大きい三角形の18cmにあたるから、3倍。
9cmの3倍だから27cm。
比例式を使って解くと、9:x=6:18
6×x=9×18
x=9×18÷6
x=27cm
(2)

(解答)12cmと9cmの辺をもつ直角三角形と、xcm、3cmの辺をもつ直角三角形とが相似です。
大きい三角形の9cmが小さい三角形の3cmにあたるから、小さい三角形は1/3。
12÷3=4cm。
比例式で解くと、9:3=12:x
9×x=3×12
x=3×12÷9
x=4cm
(3)

(解答)大きい三角形の5cmが右半分の三角形の4cm、大きいほうの4cmが右半分のxcmにあたります。
5cmと4cmの比と4cmとxcmの比が等しくなるから、小さいほうは4÷5の0.8倍。
4×0.8=3.2cm。
比例式で解くと、5:4=4:x
5×x=4×4
x=4×4÷5
x=3.2cm
最後に、よく出る、やや難しい問題にチャレンジしてみましょう。
例題4:堤防の横に幅3mの道路があり、道路にそって高い木と低い木が立っています。高い木の影が堤防の上にも1mのびています。また、低い木の高さは1.5mで、その影の長さは2mでした。堤防の影の長さは1.6mでした。高い木の高さは何mですか。

(解答)まず、堤防の高さを求めます。
小さい木とその影でできた三角形と、堤防とその影でできた三角形の形が等しいので、2:1.6と1.5:堤防の高さの比が等しくなります。
1.6÷2=0.8倍。
1.5×0.8=1.2m。
比例式だと2:1.6=1.5:x
x=1.6×1.5÷2=1.2m
 堤防がなかったらできたであろう影の図を書いてみるのがコツです(左の赤で示した図)。
堤防がなかったらできたであろう影の図を書いてみるのがコツです(左の赤で示した図)。
底辺が5.6mの三角形ができます。
赤色で書いた大きな三角形と、低い木とその影でできた小さい三角形とが相似です。
小さい三角形の2mが大きい三角形の5.6mにあたりますから、大きい三角形は5.6÷2=2.8倍。
高い木の高さは、1.5×2.8=4.2m。
比例式だと、2:5.6=1.5:x
x=5.6×1.5÷2
x=4.2m
算数の全目次はこちら
小学校 算数 分野別学習目次
辺の長さは違っても角度がそれぞれ等しいとき、2つの三角形は形が等しいといえます。
そして、形が等しいとき、2つの三角形の辺の比は等しくなります。
例題1:2つの三角形の形が等しいとき、xの値を求めなさい。
 図で、同じ色の角は角度が等しいことを表わしています。角度の等しい三角形は、形が等しいといえます。形が等しいとき、対応する辺の比も等しくなります。
図で、同じ色の角は角度が等しいことを表わしています。角度の等しい三角形は、形が等しいといえます。形が等しいとき、対応する辺の比も等しくなります。(2つの角の大きさが等ければ、三角形の3つの角の和は180度なので、色のついていない角どうしも同じ大きさです。)
左の三角形の12cmが、右の三角形だと18cmにあたりますから、右の三角形の辺の長さは左の三角形の辺の18÷12=1.5倍です。
だから、xは8×1.5=12cm。
比例式を使って解くのもよい方法です。
12:18=8:x
比例式では、内側同士の積と外側同士の積は等しいので
12×x=18×8
x=18×8÷12
x=12
例題1の2つの三角形は、見ただけですぐに形が等しい(相似)とわかりますが、気づきにくいもののほうがよく出題されます。
形が等しい三角形を見つけるコツは、角の等しい三角形を発見することです。
例題2:次の図形で、どの三角形とどの三角形の形が等しいか(=相似か)、見つけてください。
1、
 平行に気づき、等しい角を見つける(その1)
平行に気づき、等しい角を見つける(その1)左の図で、赤色の直線どうしは平行です。どの図形とどの図形が相似でしょうか?
 平行な2本の直線があるとき、等しい角を見つけておきます。
平行な2本の直線があるとき、等しい角を見つけておきます。左下の角どうし、右下の角どうしが等しくなります(同位角といいます。頂上の角も共通な角なので等しくなります。)
角度が等しいので、小さい三角形と大きい三角形の形が等しくなります。
2、
 平行に気づき、等しい角を見つける(その2)
平行に気づき、等しい角を見つける(その2)左の図の四角形は長方形(正方形でも考え方は同じ)です。
左の図の中には、お互いの形が等しい三角形の組が3組あります。見つけてください。
 1番の問題と同じ要領で、平行な2本の直線を手がかりに、等しい角をもつ三角形どうしを見つけます。
1番の問題と同じ要領で、平行な2本の直線を手がかりに、等しい角をもつ三角形どうしを見つけます。左の3組が、形の等しい三角形の組み合わせになります。
赤色と赤色、青色と青色の角どうしが等しい角です(さっ角といいます)。
1番と違い、ここで見つけた図形は、問題を解くときに、形が等しいこと、比を使えることに気づきにくいものばかりです。ある程度問題数をこなして、問題に慣れることが必要です。
3、
 直角三角形で、等しい角を見つける
直角三角形で、等しい角を見つける左の図の中には、形の等しい三角形が何個あるでしょうか?
 直角で1つの角が等しくなり、あと1つ、角が共通であれば、すべての角が等しいことになります。
直角で1つの角が等しくなり、あと1つ、角が共通であれば、すべての角が等しいことになります。つまり、直角三角形の中にある直角三角形は、すべて、もとの三角形と相似です。
では、確認問題をしてみましょう。
例題3:次の図形で、辺xの長さはいくらになりますか。
(1)

(解答)形の等しい三角形どうしの辺を考えないといけません。12cmは三角形の辺ではありません。大きな三角形の辺は6+12=18cmです。
小さい三角形の6cmが大きい三角形の18cmにあたるから、3倍。
9cmの3倍だから27cm。
比例式を使って解くと、9:x=6:18
6×x=9×18
x=9×18÷6
x=27cm
(2)

(解答)12cmと9cmの辺をもつ直角三角形と、xcm、3cmの辺をもつ直角三角形とが相似です。
大きい三角形の9cmが小さい三角形の3cmにあたるから、小さい三角形は1/3。
12÷3=4cm。
比例式で解くと、9:3=12:x
9×x=3×12
x=3×12÷9
x=4cm
(3)

(解答)大きい三角形の5cmが右半分の三角形の4cm、大きいほうの4cmが右半分のxcmにあたります。
5cmと4cmの比と4cmとxcmの比が等しくなるから、小さいほうは4÷5の0.8倍。
4×0.8=3.2cm。
比例式で解くと、5:4=4:x
5×x=4×4
x=4×4÷5
x=3.2cm
最後に、よく出る、やや難しい問題にチャレンジしてみましょう。
例題4:堤防の横に幅3mの道路があり、道路にそって高い木と低い木が立っています。高い木の影が堤防の上にも1mのびています。また、低い木の高さは1.5mで、その影の長さは2mでした。堤防の影の長さは1.6mでした。高い木の高さは何mですか。

(解答)まず、堤防の高さを求めます。
小さい木とその影でできた三角形と、堤防とその影でできた三角形の形が等しいので、2:1.6と1.5:堤防の高さの比が等しくなります。
1.6÷2=0.8倍。
1.5×0.8=1.2m。
比例式だと2:1.6=1.5:x
x=1.6×1.5÷2=1.2m
 堤防がなかったらできたであろう影の図を書いてみるのがコツです(左の赤で示した図)。
堤防がなかったらできたであろう影の図を書いてみるのがコツです(左の赤で示した図)。底辺が5.6mの三角形ができます。
赤色で書いた大きな三角形と、低い木とその影でできた小さい三角形とが相似です。
小さい三角形の2mが大きい三角形の5.6mにあたりますから、大きい三角形は5.6÷2=2.8倍。
高い木の高さは、1.5×2.8=4.2m。
比例式だと、2:5.6=1.5:x
x=5.6×1.5÷2
x=4.2m
算数の全目次はこちら
小学校 算数 分野別学習目次










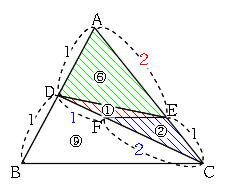






 このままでは求められません。
このままでは求められません。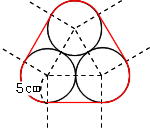 左のように線を引くと、おうぎ形と直線部分に分けることができます(直線部分に垂直な半径を書いてみるのがコツです)。
左のように線を引くと、おうぎ形と直線部分に分けることができます(直線部分に垂直な半径を書いてみるのがコツです)。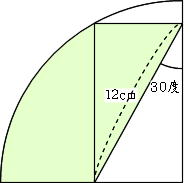 このままでは、求めることはできません。
このままでは、求めることはできません。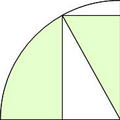 このように移動すると、おうぎ形が見えてきました。
このように移動すると、おうぎ形が見えてきました。 これでOK。
これでOK。


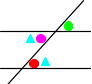 緑とピンクが等しい(対頂角)
緑とピンクが等しい(対頂角)













 左図のように、先に計算するべき場所から囲んでいき、外から逆算で求めていくほうが、まだわかりやすい。
左図のように、先に計算するべき場所から囲んでいき、外から逆算で求めていくほうが、まだわかりやすい。